- Duc Bui
Software Engineer, Monetization Team
- Tuan Anh
Former Software Engineer, Monetization Team
Introduction
Problem formation
Count-distinct problem [1], also known as the cardinality estimation problem, is a common problem in computer science that finds the number of distinct elements in a data stream. Some examples of this problem might refer to observing the IP addresses within a given time window of Internet traffic, anomaly detection on the network, etc.
In the Cốc Cốc advertising system, we would like to report the number of unique users who have seen a specific advertisement over a specified date period to measure the efficiency of ads campaigns. From the advertisers' side, they might prefer their campaigns to spread to more browser users, so there is a higher possibility that users click on or take action on their ads. From Cốc Cốc’s side, we also need to monitor this number to make sure that we do not show too many repeated adverts to one browser so make annoy users.
Definition
Input: A stream of elements x1, x2, …, xN. Each element includes the id as well as the received_date of that element. The id of these elements might be repeated through the streams.
Output: given a date period from start_date to end_date, compute the number of distinct ids (cardinality) over this period.
For example, if we have the stream: a, b, a, c, d, b, d (received_date = 2021-11-09); d, b, d, a (received_date = 2021-11-10).
The cardinality for 2021-11-09 is n = |{a,b,c,d}| = 4 , for 2021-11-10 is n = |{a,b,d}| = 3 , while for the range between 2021-11-09 and 2021-11-10 is n = |{a,b,c,d}| = 4 .
In the Cốc Cốc advertising system, we store show click events of users in the Clickhouse database, so the naive approach would be to query from the database directly like this:
| 1 SELECT COUNT(DISTINCT(id)) |
| 2 FROM statistics_table |
| 3 WHERE received_date BETWEEN start_date AND end_date |
Challenges
Before proceeding to discuss related solutions, let us consider the issues with the count-distinct problem when dealing with massive data streams.
First, counting distinct elements in massive data is heavy computation. To output the number of distinct users given a specified time range, we do not have any choice except to loop over all the elements in the multiset. Also, this naive approach consumes lots of memory to store the unique ids in every time frame. For example, if we count the number of unique users in 2 days, then we have to use 2 hash sets and store the unique user ids in each day. This issue gets more problems in case of storing data on disk and on multiple machines which are typical with most sharded databases.
Given those challenges, counting the exact number of distinct users is impossible in a large-scale application. The natural way is to find an approximation algorithm to solve the count-distinct problem. In the following section, we will survey some existing algorithms which use significantly less memory and gain high accurate estimation. One of them is used in Cốc Cốc Advertising system to monitor the advertising effectiveness as well as satisfy browser users.
History and some existing algorithms
All of the three algorithms in this section are based on probabilistic counting. To keep this article short, we will not introduce the probabilistic theory. Like many approximation algorithms, the basic idea is to find a hash function in order to randomize data. In the case of a count-distinct problem, we try to find a hash function that can resemble data as uniform distribution.
♦ Flajolet-Martin algorithm
Given a multiset of M elements, we assume that the cardinality (the number of unique elements in this multiset) is L. We will try to find a hash function h(x) which maps input x to the integers in [0; 2^L - 1]. The simplest hash function is the binary representation of x (length L). The algorithm also uses the function p(y) which represents the position of the least significant 1-bit in the binary representation of y.
The intuition is that if function hash(x) are uniformly distributed, the binary string 000…0111…1 (k-digit 0) appears with probability 1 / 2 ^ (k + 1). You can find the related theory and the proof in the original paper which is introduced in [1].
Algorithm
| 1 1. Init a bit vector BITMAP[L] := [0] * L |
| 2 2. For all x in multiset M do |
| 3 index := p(hash(x)) |
| 4 BITMAP[index] = 1 |
| 5 3. R := smallest index s.t BITMAP[index] = 0 |
| 6 4. Return cardinality := 2^R / 0.77351 |
Notice that vector BITMAP only depends on the set of hashed values and not on a particular repeated frequency. If n is the number of distinct elements in M, we should expect that BITMAP[0] is accessed approximately n/2 times, BITMAP[1] is accessed approximately n/4 times,… Therefore, if i >> log(n), BITMAP[i] will almost certainly be zero, and BITMAP[i] is 1 if i << log(n) on the other hand.
♦ Improving accuracy by LogLog algorithm
Although the Flajolet-Martin algorithm uses less memory and runs much faster than the count exactly approach, its high variance is not that great. The LogLog algorithm improves accuracy by using a better hash function.
Overall, it maps the binary numbers computed from hash function h(x) to m buckets, then stores the median of each group. The final approximation will be the average of all the medians. This approach is also known as stochastic average. You can find the original paper in [2].
Algorithm
| 1 1. Init a vector of m buckets BUCKET[m] := [0] * m |
| 2 # m = 2 ^ k |
| 3 2. For all x in multiset M do |
| 4 # assume b1b2...b_N is binary representation of x |
| 5 j := b1b2...b_k (first k bits of x) |
| 6 w := b_(k+1), ..., b_N (remained bits) |
| 7 BUCKET[j] = max(BUCKET[j], p(w)) |
| 8 3. Return cardinality := alpha * m * 2 ^ (-m) * (sum of BUCKET) |
Here, alpha is constant and defined as:
| 1 alpha = (gamma(1 / M) * (2 ^ (-m) - 1) / log2 ) ^ (-m) |
The idea and proof of this algorithm are introduced in [2]. In this algorithm, the author is trying to reduce the standard error of the approximation. It is proved that the error rate of the LogLog algorithm should be around 1.3 / square(m).
♦ HyperLogLog algorithm
HyperLogLog is an extended version of the LogLog algorithm with a standard error of around 1.04 / square(m). It also consumes only 64% of memory compared to the LogLog algorithm, as pointed out in the original paper.
The HyperLogLog has three main operations: add, count, and merge. The space complexity for HyperLogLog is O(log(log(n)), while time complexity depends on operation.
- Add operation: Add a new element to the set. O(1) time complexity,
- Count operation: obtain the cardinality of the set. O(m) time complexity.
- Merge operation: the union of N sets. O(N * m) time complexity.
Algorithm
| 1 # assume m = 2 ^ k |
| 2 # register is similar to bucket as in LogLog |
| 3 1. Init m registers, R[m] := [INT_MIN] * m |
| 4 2. For all x in multiset M do |
| 5 b := h(x) |
| 6 j := 1 + b1b2...b_k (first k bits of x) |
| 7 w := b_(k+1), ..., b_N (remained bits) |
| 8 R[j] = max(R[j], p(w)) |
| 9 3. Compute indicator Z := (2 ^ (-R[0]) + 2 ^ (-R[0]) + ... + 2 ^ (-R[m - 1])) |
| 10 4. Return cardinality := alpha * m^2 * Z |
As we can see, HyperLogLog is an extended version of the LogLog algorithm. The alpha constant in step 4 is harder to choose and you can refer to the original paper at [3] for some recommendations. This change helps to improve the LogLog algorithm with higher accuracy and less memory consumption. From the author’s experimentation, the HyperLogLog algorithm is able to estimate cardinalities of > 109 with a typical accuracy (standard error) of 2%, using 1.5 kB of memory.
Example in Ads System
In this section, we provide a simple solution to the count-distinct problem in the Cốc Cốc Advertising system, e.g., count the unique number of users viewing an advertisement from start_date to end_date by using HyperLogLog Redis’s implementation [5].
A Redis HyperLogLog consumes at most 12 kilobytes of memory and produces approximations with a standard error of 0.81%. The 12 kilobytes do not include the bytes required to store the actual key.
The HyperLogLog data structure is available in Redis via the PFADD, PFCOUNT, and PFMERGE commands.
PFADD adds all the arguments provided to the HyperLogLog data structure with the key specified as the first argument.
If the item count estimated by HyperLogLog is changed after the command is executed, PFADD returns 1; otherwise, it returns 0.
PFCOUNT returns the approximate item count stored by the HyperLogLog data structure that is specified by the key provided as the first argument.
If multiple keys are provided, PFCOUNT internally merges the HyperLogLogs stored at the provided keys into a temporary HyperLogLog. Then, it returns the approximate count of the union of HyperLogLogs passed.
| 1 > PFADD key a b c d e f g |
| 2 (integer) 1 |
| 3 > PFCOUNT key |
| 4 (integer) 7 |
PFMERGE merges multiple source HyperLogLog values into a unique value that will approximate the count of the union of the sets of the source HyperLogLog data structures.
| 1 # assume m = 2 ^ k |
| 2 # register is similar to bucket as in LogLog |
| 3 1. Init m registers, R[m] := [INT_MIN] * m |
| 4 2. For all x in multiset M do |
| 5 b := h(x) |
| 6 j := 1 + b1b2...b_k (first k bits of x) |
| 7 w := b_(k+1), ..., b_N (remained bits) |
| 8 R[j] = max(R[j], p(w)) |
By using this feature of Redis, we can solve the count-distinct problem with this simple pipeline:
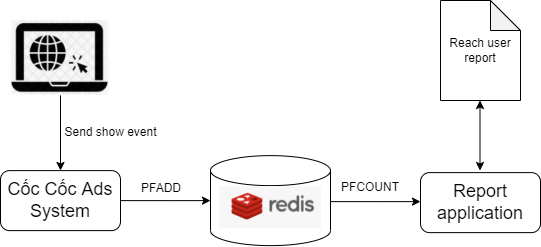
Add operation
Cốc Cốc Ads system generates a key for each campaign id and the received date when it receives a show event from the user. Add browser id of this event as a new element of this key with PFADD command. For example, when the system receives an event that browser id user1 viewed the advertisement of campaign id campaign1, it sends this command to Redis:
| 1 > PFADD {campaign1}:2021-12-30 user1 |
| 2 (integer) 1 |
As running PFADD command the HyperLogLog internals may be updated to reflect a different estimation of the number of unique items added so far (the cardinality of the set).
Count operation
We’ve made one service for returning cardinality estimation named unique-browser id-show-count. Whenever it received a request to return a result for campaign id campaign1 on the date 2021-12-31, it sends this command to Redis:
| 1 > PFCOUNT {campaign1}:2021-12-30 |
| 2 (integer) 1121321 |
We support return results in a time range, just add more parameters to PFCOUNT commands, Redis will merge all HyperLogLog data structures on-the-fly.
| 1 > PFCOUNT {campaign1}:2021-12-30 {campaign1}:2021-12-31 {campaign1}:2022-01-01 |
| 2 (integer) 1441222 |
We also support to return of results of multiple campaigns in a time range. To do that, multiple PFCOUNT commands must be sent in a row.
| 1 > PFCOUNT {campaign1}:2021-12-30 {campaign1}:2021-12-31 {campaign1}:2022-01-01 |
| 2 (integer) 2231122 |
| 3 > PFCOUNT {campaign2}:2021-12-30 {campaign2}:2021-12-31 {campaign2}:2022-01-01 |
| 4 (integer) 1121242 |
In order to reduce the latency of this type of request, we use a technique called Redis pipeline for ignoring the round-trip time penalty. So multiple PFCOUNT can be sent in one request to Redis.
Merge operation
When PFCOUNT is called with multiple keys, and an on-the-fly merge of the HyperLogLogs is performed, which is slow, moreover, the cardinality of the union can't be cached. We can use PFMERGE to union all keys and cache them for later use:
| 1 > PFMERGE {campaign1}:2021-12 {campaign1}:2021-12-01 {campaign1}:2021-12-02 ... {campaign1}:2021-12-31 |
| 2 "OK" |
| 3 > PFCOUNT {campaign1}:2021-12 |
| 4 (integer) 23 |
Compare with the naive solution
I tried to get the cardinality of browser id which has seen campaign id 1305626 by using Clickhouse uniqExact() function and by using Redis PFCOUNT. Here is the result:
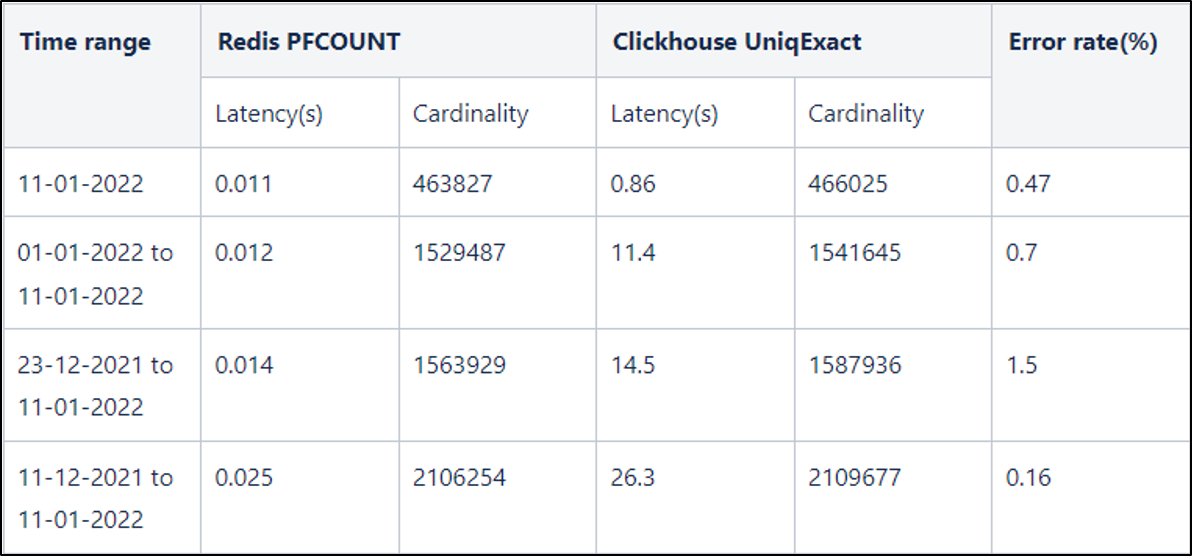
As you can see, using Redis HyperLogLog give us a big advantage in term of request latency and the error rate is quite small and can be accepted.
Sample usage in Go
| 1 package main |
| 2 |
| 3 import ( |
| 4 "context" |
| 5 "fmt" |
| 6 "time" |
| 7 |
| 8 "github.com/go-redis/redis/v8" |
| 9 ) |
| 10 |
| 11 func main() { |
| 12 // Make redis cluster |
| 13 cluster := redis.NewClusterClient(&redis.ClusterOptions{ |
| 14 Addrs: addrs, |
| 15 Password: password, |
| 16 }) |
| 17 if cluster == nil { |
| 18 fmt.Println("Error when creating cluster client") |
| 19 return |
| 20 } |
| 21 |
| 22 cids := []string{"campaign_id1", "campaign_id2", "campaign_id3", "campaign_id4", "campaign_id5"} |
| 23 pipe := cluster.Pipeline() |
| 24 |
| 25 // Add new set of user to hll data structure with key campaign_id |
| 26 for _, cid := range cids { |
| 27 pipe.PFAdd(context.TODO(), cid, "user1", "user2", "user3", "user4", "user1") |
| 28 } |
| 29 _, err := pipe.Exec(context.TODO()) |
| 30 if err != nil { |
| 31 fmt.Println("Error when executing command") |
| 32 return |
| 33 } |
| 34 |
| 35 // Get cardinality value of that hll data structure |
| 36 res := cluster.PFCount(context.TODO(), cids...) |
| 37 v, err := res.Uint64() |
| 38 if err != nil { |
| 39 fmt.Println("Error when executing command") |
| 40 return |
| 41 } |
| 42 fmt.Println("Cardinality value: ", v) |
| 43 } |
| 44 |
Reference
[1] Flajolet, Philippe; Martin, G. Nigel (1985). "Probabilistic counting algorithms for database applications" (PDF). Journal of Computer and System Sciences. 31 (2): 182–209. doi:10.1016/0022-0000(85)90041-8. Retrieved 2016-12-11.
[2] Durand, Marianne; Flajolet, Philippe (2003). "Loglog Counting of Large Cardinalities" (PDF). Algorithms - ESA 2003. Lecture Notes in Computer Science. 2832. p. 605. doi:10.1007/978-3-540-39658-1_55. ISBN 978-3-540-20064-2. Retrieved 2016-12-11.
[3] Flajolet, Philippe; Fusy, Éric; Gandouet, Olivier; Meunier, Frédéric (2007). "Hyperloglog: The analysis of a near-optimal cardinality estimation algorithm" (PDF). Discrete Mathematics and Theoretical Computer Science proceedings. Nancy, France. AH: 127–146. CiteSeerX 10.1.1.76.4286. Retrieved 2016-12-11.
[5] Redis new data structure: the HyperLogLog - <antirez>

